Bakgrund
Att skapa en labyrint är en lagom svår och utmanande uppgift om man redan har lärt sig grunderna i programmering. Det kan också vara en bra uppgift att göra när man testar ett nytt språk för första gången.
I denna artikel ska vi ge oss på att generera så kallade ”perfekta labyrinter”. En ”perfekt” labyrint är en labyrint som inte innehåller några loop’ar. Det betyder att du aldrig kan komma till ett ställe som du redan har varit på under din färd i labyrinten (om du inte vänder och går tillbaka såklart). Det betyder också att mellan två punkter i labyrinten så finns det bara en lösning. Du kan också nå alla platser i labyrinten. Om man rätar ut alla möjliga vägar i labyrinten så skulle man kunna rita dem som ett träddiagram med olika förgreningar.
Hursomhelst så finns det många olika algoritmer som löser denna uppgift åt oss redan, t.ex. Prims, Kuskals, Ellers, m.fl. Vi ska kika på algoritmen ”recursive backtracking”. Recursive backtracking är en effektiv algoritm som inte är alltför svår att förstå sig på. Jag tror det är dags att presentera hur den fungerar.
Recursive backtracking
Förutsättningarna är att vi har ett rutnät som representerar vår labyrint. Mellan alla rutorna så finns det redan väggar. Vi ska karva ut en labyrint genom att ta bort väggar.

De svarta linjerna representerar väggar och de gråa rutorna är celler som vi ännu inte besökt.
Algoritmen arbetar såhär:
- Välj en startpunkt i labyrinten.
- Välj slumpvis en vägg till en intilliggande cell i labyrinten som du inte redan har besökt. Detta blir den nya punkten du står på.
- Om alla intilliggande celler redan är besökta så får vi backa till den senaste besökta cellen längs vägen som har väggar som leder till nya celler. Upprepa från #2.
- Algoritmen slutar när vi har backat tillbaka till utgångspunkten.
Nu ska vi se hur algoritmen jobbar. Vi kommer använda beteckningarna för väderstreck N (upp), E (höger), W, (vänster), S (nedåt) för att beskriva riktningar.
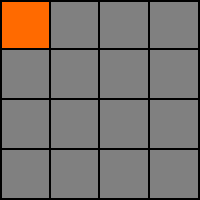
1. Välj en valfri cell. I vårt exempel längst upp till vänster (0,0). Orange markerar celler som befinner sig på den väg vi håller på att skapa.
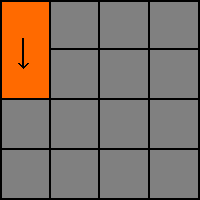
2. Nu slumpar vi mellan de intilliggande celler som vi inte redan besökt. De vi har att välja på är S och E. Vi väljer S (0,1) och tar bor väggen till denna cell och flyttar fram.
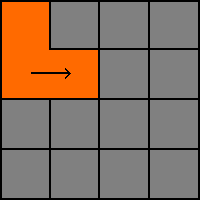
3. Vi upprepar och väljer denna gång E (1,1) som riktning. River väggen och flyttar till den nya cellen.
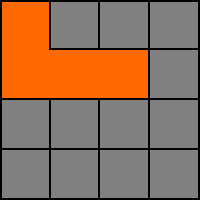
4. Vi upprepar igen och väljer åter E (2,1) som riktning. River väggen och flyttar till den nya cellen.
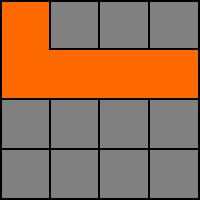
5. Vi väljer E (3,1) .
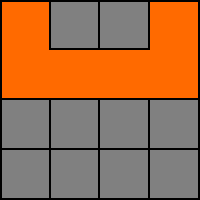
6. Vi väljer N och framöver nu så finns det inga möjligheter att välja väg.
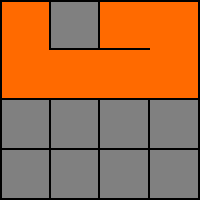
7. W.
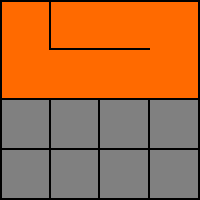
8. W. Nu har vi hamnat i en återvändsgränd. I nästa steg måste vi ”backtrack’a” till en cell längs den orange’a vägen som erbjuder nya vägar.
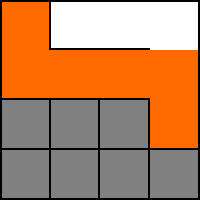
9. Vi går tillbaka (”backtrack”) till ruta (3,1) och hittar en ny väg S (3,2). De vita cellerna är nu besökta och ligger inte längre längs vår orange’a väg.
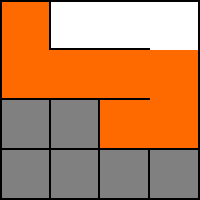
10. Vi väljer W.
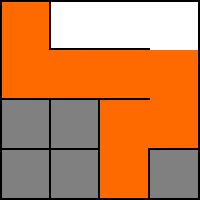
11. S.
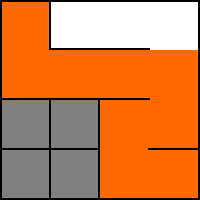
12. E. Nu hamnar vi i en återvändsgränd igen.

13. Vi går tillbaka (”backtrack”) till ruta (2,3) och hittar en ny väg W (1,3). De vita cellerna är nu besökta och ligger inte längre längs vår orange’a väg.
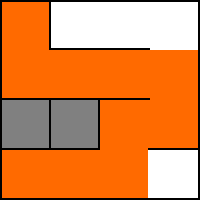
14. W.

15. N.

16. E. Nu har vi besökt den sista cellen i labyrinten.
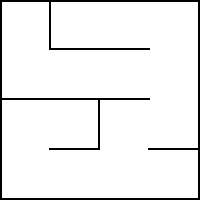
17. Nu har vi gått tillbaka längs alla orange’a rutor utan att hitta några nya vägar. Till slut har vi gått tillbaka till startpunkten (0,0) och algoritmen är klar!
Implementation
Först behöver vi lite klasser för att hantera den data som behövs för att beskriva väggar. Vi tänker oss att en ruta på spelplanen kan ha väggar i alla riktningar N,E,W,S. En lämplig lösning kan vara att använda enum för att skapa en variabeltyp, som via värden, kan beskriva alla olika kombinationer av väggar som en ruta kan tänkas ha.
Dataklasser
using System;
namespace GenerateMaze
{
[Flags]
enum Walls
{
None = 0,
N = 1,
E = 2,
W = 4,
S = 8,
All = N|E|W|S
}
}
Som du kanske märker så är Walls markerade med attributet Flags. Detta gör det lättare för oss att skapa kombinationer av väggar för en ruta. Vi ger t.ex. tillståndet None värdet 0. Sedan väljer vi binära värden för de olika riktningarna N,E,W,S. På så sätt kan vi kombinera t.ex. N+E = 3, eller E + S = 10 i samma variabel och varje tänkbar kombination av väggar kommer ge ett specifikt värde.
Att använda en enum som ”flaggor” (binära bitar) är inte helt ovanligt och ibland väldigt användbart. Som du också kanske märker så kan vi definiera speciella kombinationer av flaggorna som fasta värde, t.ex. All som då innefattar alla riktningar. Operatorerna som används är | för OR och & för AND. Detta är de så kallade ”bitvisa” operatorerna och också en förklaring till varför man använder dubbla || och dubbla && för när man konstruerar logiska uttryck. Man måste kunna skilja dessa operatorer åt.
Nu dags för klassen som ska representera en ruta på vår spelplan.
namespace GenerateMaze
{
class Block
{
public Walls Walls { get; set; }
public int X { get; set; }
public int Y { get; set; }
public bool Visited { get; set; }
public Block(int x, int y)
{
X = x;
Y = y;
Walls = Walls.All;
}
}
}
Vi kallar klassen Block. Informationen som lagras är vilka väggar som finns, Walls, vilken position ”blocket” befinner sig på, X, Y samt om vi har behandlat rutan i vår algoritm, Visited.
Givet dessa ”dataklasser” så är vi nu redo för själva algoritmen.
Algoritmen Recursive Backtracking
using System;
using System.Collections.Generic;
using System.Linq;
namespace GenerateMaze
{
class Program
{
const int size = 10;
static Block[,] map = new Block[size, size];
static Stack<Block> _stack = new Stack<Block>();
static void Main(string[] args)
{
Random rnd = new Random();
// setup map
for (int y = 0; y < size; y++)
{
for (int x = 0; x < size; x++)
{
map[x,y] = new Block(x, y);
}
}
_stack.Push(map[0,0]);
while (_stack.Count > 0)
{
var current = _stack.First();
current.Visited = true;
List<Block> potential = new List<Block>();
if(current.X - 1 >= 0 && !map[current.X-1, current.Y].Visited)
potential.Add(map[current.X-1, current.Y]);
if (current.X + 1 < size && !map[current.X + 1, current.Y].Visited)
potential.Add(map[current.X + 1, current.Y]);
if (current.Y - 1 >= 0 && !map[current.X, current.Y - 1].Visited)
potential.Add(map[current.X, current.Y - 1]);
if (current.Y + 1 < size && !map[current.X, current.Y + 1].Visited)
potential.Add(map[current.X, current.Y + 1]);
//Done?
if (potential.Count == 0)
{
_stack.Pop();
continue;
}
else
{
var next = potential[rnd.Next(potential.Count)];
_stack.Push(next);
if (next.X > current.X)
{
current.Walls &= ~Walls.E;
next.Walls &= ~Walls.W;
}
else if (next.X < current.X)
{
current.Walls &= ~Walls.W;
next.Walls &= ~Walls.E;
}
else if(next.Y > current.Y)
{
current.Walls &= ~Walls.S;
next.Walls &= ~Walls.N;
}
else if (next.Y < current.Y)
{
current.Walls &= ~Walls.N;
next.Walls &= ~Walls.S;
}
//DrawMap();
//Console.WriteLine($"X={current.X} Y={current.Y}");
//Console.WriteLine($"Next X={next.X} Y={next.Y}");
//Console.ReadKey();
}
}
DrawMap();
Console.ReadKey();
}
}
}Fram till rad #27 är det bara initialisering. Vi bestämmer att spelplanen ska vara 10×10 i storlek och skapar en variabel, map, som är vår spelplan. Vi ser sedan till att det finns ett Block på varje position på spelplanen där alla rutor har väggar i alla riktningar.
På rad #27 lägger vi in startpunkten för vår vandring i labyrinten. I exemplet är det position (0,0) men det skulle kunna vara vilken position som helst på spelplanen.
Med hjälp av vår variabel _stack, kommer vi att kunna hålla reda på vilken väg vi har vandrat i labyrinten. ”Stacken” som vi använder här kommer att ha samma funktion datorn egen stack (”Call Stack”) har i ett program. När du debuggar ett program har du säkert sett ”Call Stack” informationen. Den talar om vilka metoder ditt program har anropat och visar på så vis vilken väg programmet har tagit för att hamna där den är just nu.
Vi skulle kunna implementera algoritmen rekursivt och använda ”Call Stack”’en som stack men genom att använda en egen stack så slipper vi rekursiviteten. En rekursiv implementation är oftast svårare att följa och syftet med artikeln är att lära ut själva algoritmen.
Viktigt att känna till om lagringsklassen Stack;
Push() lägger något på ”högen” och Pop() plockar något överst (det senaste) från högen samtidigt som det tas bort från ”högen”.
Loop’en (rad #29) håller algoritmen igång så länge det finns rutor vårt stack som ska behandlas. Från start finns det alltså en ruta i listan. Den senaste rutan i listan plockas ut (rad #31), den markeras som besökt och sedan behöver vi skapa en temporär lista på vilka möjliga rutor vi kan nå (som inte redan är besökta). Genom att undersöka alla intilliggande rutor, och samtidigt kolla så vi håller oss inom spelplanen samt att rutorna inte redan är besökta, så läggs rutorna i listan potential (rad #35-42).
Om listan visar sig vara tom (rad #45) så är det en återvändsgränd. I så fall slänger vi rutan från stacken med Pop() och börjar om loop’en. Annars så gör vi en lottdragning från potential (rad #52) och går till en ny ruta, som vi genast lägger i stacken. Tänk på stacken som vår väg genom labyrinten.
När vi nu vet vilken ruta vid stod på (current) samt vilken vi går till (next) så ska vi öppna upp väggarna däremellan. Beroende på vilken riktning vi färdas så måste rätt väggar tas bort mellan rutorna. Detta görs på raderna 55-74 i koden. Här blir det lite bit-jonglering. Operatorn &= betyder i praktiken ”bit för bit, släck alla bitar där det finns en 0’a till höger”. Operatorn ~ betyder invertering, alltså alla bitar som är 0 blir 1 o vice versa. Genom att t.ex. ange ~Walls.E till höger så betyder det ”släck biten E” eftersom alla andra bitar är 1.
Just här har vi ett bra exempel på varför man ska undervisa Boolesk algebra inom t.ex. matematik eller teknik. Genom att bättre förstå bitar och bit-operationer så kan man koda och förstå hur en dator jobbar bättre. Fördelen att använda bitar för väggarna är, dels kan vi lagra all information i en variabel och sedan möjliggör vi också att koden kan göras än mer kompakt o effektiv.
Uppritning
Det som saknas är en metod för DrawMap. När det gäller labyrinter så finns det två sätt att rita upp dem på. Man kan välja att rita väggarna som ”tunna” väggar precis som bilder längre upp i artikeln. Ibland vill man kanske låta väggarna i sig ta upp en hel rita på spelplanen. När vi ska försöka rita upp labyrinten i ett Console Application så blir det svårt med ”tunna” väggar. Därför har vi valt att implementera DrawMap med ”tjocka” väggar.
static void DrawMap()
{
Console.Clear();
// Draw map
for (int y = 0; y < size; y++)
{
//Walls
for (int x = 0; x < size; x++)
{
if (map[x, y].Walls.HasFlag(Walls.N))
Console.Write("***");
else
if (map[x, y].Walls.HasFlag(Walls.W))
Console.Write("* ");
else
Console.Write(" ");
}
Console.WriteLine("*");
for (int x = 0; x < size; x++)
{
if (map[x, y].Walls.HasFlag(Walls.W))
{
if (_stack.Any(b => b.X == x && b.Y == y))
{
Console.Write("*");
Console.BackgroundColor = ConsoleColor.Blue;
Console.Write(" ");
Console.BackgroundColor = ConsoleColor.Black;
}
else
{
Console.Write("* ");
}
}
else
{
if (_stack.Any(b => b.X == x && b.Y == y))
{
Console.Write(" ");
Console.BackgroundColor = ConsoleColor.Blue;
Console.Write(" ");
Console.BackgroundColor = ConsoleColor.Black;
}
else
Console.Write(" ");
}
}
Console.WriteLine("*");
}
Console.WriteLine(new String('*', size * 3 + 1));
}Metoden ska erkännas är inte speciellt snygg men den gör sitt jobb. Problemet är att typsnittet i Console är smalt så därför måste man skriva ut ett extra tecken i bredd för att kompensera. Metoden ritar också ut en blå bakgrund för att visa aktuell väg om man väljer att skriva ut algoritmen ”steg för steg”.
Man kan alltså visualisera samma data på två sätt, antingen med ”tunna” väggar, som tidigare i artikeln, eller som ”tjocka” väggar, se bilder nedan.

Vi börjar längst upp till vänster (0,0) och har grävt en några steg. De blåa rutorna visar vilken väg vi har följt. Det kan vara lite svårt att se.

Här har vi besökt hela den övre högra delen av labyrinten redan och ”vänt tillbaka” några gånger redan.
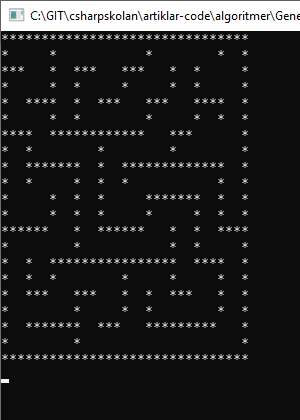
Slutresultat.
Sammanfattning
I metoden DrawMap används en metod kallad HasFlag för att kolla ”flaggor” eller bitar på vår enum. Tyvärr finns det ingen metod SetFlag eller ClearFlag. Men sådana metoder kan man själv lägga till genom ”Extension methods”. Det hade gjort koden än mer lättläst.
Recursive backtracking skulle man kunna klassificera som en sökalgoritm. Säg t.ex. att man redan har en labyrint som du ska hitta ur, hur gör du då? Jo recursive backtracking löser problemet, även om det inte skulle råka vara en ”perfekt” labyrint.
Med detta i bagaget så kan du nu generera egna ”dungeons” eller liknande i dina framtida spel. Lycka till!

Senaste kommentarer